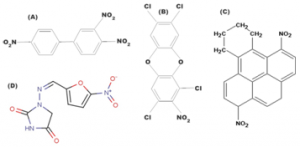
Consider the dataset given in the figure below, a set of compounds that could be found in the NCI repository, for example. The learning task associated with this dataset is to build a model using molecules that are already labeled as mutagenetic or not, so that the model can be used to label previously unseen molecules.
Figure 3:(A) 3,4,4′-trinitrobiphenyl (B)2-nitro-1,3,7,8-tetrachlorodibenzo-1,4-dioxin (C) 1,6,-dinitro-9,10,11,12-tetrahydrobenzo[e]pyrene (D) nitrofurantoin
How can we learn from such graph data? Experts from specific domains use their own methods for representing the graph data as a fixed-length feature set that could be used in learning from graph data in the particular domain. Common approach is to find certain properties from the respective domain and represent the graphs as a fixed-length feature vector in terms of these properties. For example, in the chemoinformatics domain, the domain specific approaches include (1) extracting relevant structural information of compounds, and (2) building the predictive model using the structural information encoded as attributes. The structural information can be represented by various structure-based theoretical estimates of properties of compounds, which are commonly referred to as (chemical) descriptors. These descriptors are twofold; (experimentally derived) properties-based and (topological) structure-based. The former include global properties of molecules, such as their weight, number of atoms and bonds, various atomic measures, number of pre-identified substructures, e.g., carbons rings, and so forth. Several such descriptor sets have been developed within the field of chemoinformatics, capturing various properties of molecules (Mahe, 2006). The SELMA descriptor set (Olsson & Sherbukhin, 1999) is an example of such a collection of descriptors. Descriptors that represent the topological structure of a molecule usually transform the 2D or 3D structure of the molecule into a set of single-valued descriptors, e.g., ECFI (Rogers & Hahn, 2010), characterizing structures with respect to their size, degree of branching, overall shape, etc. Some such descriptors are derived from 2D representations of molecules in the form of strings, such as SMILES and SMARTS (Daylight , 2007). However, this fixed-length feature vector representation ignores graph structure of molecules allowing fewer chances to exploit any special properties of graphs of different datasets.
The existing techniques that could be used to solve similar problems irrespective of the domain the graphs belong to, typically upgrade from this fixed-length propositional form and focus on dealing with the richer representational setting. Within these techniques a number of paradigms could be identified each of which is inspired by an existing and well-known choice for representing and manipulating graphs (Han & Kamber, 2001). Two main forms of learning tasks can be found in the literature, namely, model building and pattern discovery. Model building methods use different characteristics of data elements to learn from them, for example, similarity between pairs of data elements in the dataset can be used as a measure for building models. An example of such approach is the kernel based methods (Vishwanathan, et al., 2010; Borgwardt & Kriegel, 2005; Horváth, et al., 2004; Gärtner, 2008), which aims at computing different kernels that reflects the similarities between (graph) data in the dataset. These kernels usually generate global models for classifying all examples. However graph similarity based methods require finding kernel functions that perform well for a given dataset, which has become a challenge for these approaches (Gärtner, 2008). Similarity based methods usually apply one chosen machine learning algorithm (typically support vector machines (Platt, 1998)) in their model building limiting the flexibility of choosing the learning algorithm. The advantage of such flexibility is discussed in a subsequent section.
Methods that use pattern sets as features for learning represent graphs in terms of attribute-value pairs. There are two forms of such representation, namely, global models and pattern sets. Manila (2002) describes these forms as finding models using a probabilistic approach and using fast counting to discover patterns from graph data and use these patterns as attributes in propositional form to build models using a machine learning algorithm. In Bringmann (2009) these two approaches are simply referred to as models and patterns, assuming models summarizes the dataset, while patterns concern localized chunks that satisfy a predefined interestingness measure on a subset of the dataset.
The probabilistic approaches try fitting the data into a known parametric distribution. This approach is very useful due to the fact that once the underlying distribution of the data is discovered; any statistic related to unseen data elements can be drawn from the distribution (Han & Kamber, 2001). However, discovering such a distribution is challenging, since most of the real world data in no way fit into such models, or at least strong assumptions should be imposed on the data during the pre-processing or model building (Manila, 2002) in order to obtain such models. Finding feature sets that could be used as fixed-length feature vector to the learning models is an alternative to fitting data into probability distributions. In this approach, important characteristics of the datasets or the domain are used to encode graphs as attribute-value pairs. These attributes are usually domain specific, for example, in a chemoinformatics domain, carbon atoms count, molecular weight, etc., could be considered as attributes. Further, in this approach, feature set is fixed, i.e., size of the feature vector used in the model building is same for any dataset. As a consequence features that are very useful in making predictions with respect to one dataset may be completely irrelevant in another dataset, which is a drawback of this approach.
The approach of discovering patterns from graph data that employs fast counting techniques on data to discover aggregated information (Kriegel, et al., 2007) is a localized pattern discovery approach, which is commonly referred to as (graph) pattern mining. In contrast to the feature vectors of global models, the patterns (which are treated as the feature set for learning), depend on the dataset, i.e., different datasets discover different pattern sets thereby the length of the feature vector varies from one dataset to another. Machine learning methods, which use patterns as features in attribute-value (propositional) format, apply several techniques for selecting a set of most important features (Cook & Holder, 1994; Borgelt & Berthold, 2002; Bringmann & Zimmernann, 2005; De Raedt & Kramer, 2001; Hasan & Zaki, 2009; Helma, et al., 2002), and thereby use these features in a propositional learner to build the predictive models. Graphs could be transformed into logic programs (Qunilan & Cameron-Jones, 1993; Srinivasan, et al., 1999; Muggleton & Feng, 1992; Yan & Han, 2002; Huan, et al., 2004). This approach allows the graphs to be represented in first or higher order logic, and a logic program is used for (inductive) learning from the data. Inductive Logic Programming (ILP) methods either produce a model with a set of association rules, or discover a set of features that could be represented in propositional language (Lavrac, et al., 2002; Helma, et al., 2002; Flach & Lachiche, 1999; Kramer & Frank, 2000; Krogel, et al., 2003). Even though the approach of pattern mining has two steps, i.e., discovery of patterns and model building, it has an advantage over the global models that any machine learning algorithm could be used for model building, due to the fact that discovered patterns can be represented in the propositional format which is recognized by most of the machine learning algorithms. Having a flexibility of choosing the learning algorithm is advantageous since machine learning algorithms possess tradeoff between the comprehensibility (how far the discovered models could be comprehended by domain experts) and the predictive performance (Cook & Holder, 2006). With such flexibility one could be able to choose a learning algorithm such as decision trees (Quinlan, 1993) if the task requires highly comprehensible models, while the Support Vector Machine (Platt, 1998) or random forest algorithm (Breiman, 2001) could be used for tasks that prioritize higher accuracy over comprehensibility.